Přednášky trojný integrál. Trojný integrál ve cylindrických souřadnicích Přechod na cylindrické souřadnice vypočítejte trojný integrál

Transformace dvojného integrálu pravoúhlých souřadnic, na polární souřadnice
, vztahující se k pravoúhlým souřadnicím vztahem
,
, se provádí podle vzorce

Pokud doména integrace
omezena na dva paprsky
,
(
), vycházející z tyče a dvě křivky
A
, pak se dvojný integrál vypočítá pomocí vzorce

.

Příklad 1.3. Vypočítejte plochu obrázku ohraničenou těmito čarami:
,
,
,
.

Řešení. Pro výpočet plochy plochy
Použijme vzorec:
.

.

1.2. Trojné integrály

Základní vlastnosti trojné integrály podobné vlastnostem dvojných integrálů.

V kartézských souřadnicích se trojný integrál obvykle zapisuje takto:

.

Li
, pak trojný integrál nad plochou číselně se rovná objemu tělesa :

.

Výpočet trojného integrálu

Nechť doménu integrace ohraničené pod a nad jednohodnotovými spojitými plochami
,
a projekce regionu do souřadnicové roviny
je tam rovná plocha
(obr. 1.6).

.

Příklad 1.4. Vypočítat
, Kde - těleso ohraničené rovinami:

Trojný integrál ve cylindrických souřadnicích

Při pohybu z kartézských souřadnic
na cylindrické souřadnice
(obr. 1.9) spojené s
vztahy
,
,
, a

Kraj
, ohraničený křivkou
, bude mít podobu, popř
, zatímco polární úhel
. V důsledku toho máme

.

2. Základy teorie pole

Nejprve si připomeňme metody výpočtu křivočarých a plošných integrálů.

Výpočet křivočarého integrálu přes souřadnice funkcí definovaných na křivce , redukuje na výpočet určitého integrálu tvaru

pokud křivka specifikováno parametricky
odpovídá počátečnímu bodu křivky , A
- jeho koncový bod.

Výpočet plošného integrálu funkce
, definovaný na oboustranném povrchu , dojde k výpočtu dvojného integrálu, například tvaru

pokud povrch , daný rovnicí
, se jedinečně promítá do roviny
do regionu
. Tady - úhel mezi jednotkovým normálovým vektorem na povrch a osa
:

Strana povrchu požadovaná problémovými podmínkami je určena volbou příslušného znaménka ve vzorci (2.3).

Definice 2.1. Vektorové pole
nazýváme vektorovou funkcí bodu
spolu s jeho rozsahem:

Vektorové pole
charakterizované skalární veličinou – divergence:

Definice 2.2. Tok vektorové pole
přes povrch nazývá se povrchový integrál:

Kde - jednotkový normálový vektor na vybranou stranu povrchu , A
- skalární součin vektorů A .

Definice 2.3. Oběh vektorové pole

Podle uzavřená křivka nazývaný křivočarý integrál

Kde
.

Ostrogradského-Gaussův vzorec vytváří spojení mezi tokem vektorového pole přes uzavřený povrch a divergence pole:

Kde - povrch ohraničený uzavřeným obrysem , A je jednotkový normálový vektor k tomuto povrchu. Směr normály musí být v souladu se směrem přechodu obrysu .

Příklad 2.1. Vypočítat integrál povrchu

,

Kde - vnější část kužele
(
), odříznutý letadlem
(Obrázek 2.1).

Řešení. Povrch jedinečně promítnuté do regionu
letadlo
a integrál se vypočítá pomocí vzorce (2.2).

Kraj
je tam kruh
. Proto se v posledním integrálu přesuneme na polární souřadnice, while
,
:

Příklad 2.2. Najděte divergenci a zvlnění vektorového pole
.

Řešení. Pomocí vzorce (2.4) získáme

Rotor daného vektorového pole se najde pomocí vzorce (2.5)

Příklad 2.3. Najděte tok vektorového pole
přes část letadla :
, umístěný v prvním oktantu (normální formy ostrý roh s nápravou
).

Kde
- rovinná projekce na
(obr. 2.4).

Příklad 2.4. Vypočítejte tok vektorového pole uzavřeným povrchem , tvořený rovinou
a část kužele
(
) (obr. 2.2).

Řešení. Použijme Ostrogradského-Gaussův vzorec (2.8)

.

Pojďme najít divergenci vektorového pole podle vzorce (2.4):

Kde
je objem kužele, přes který se provádí integrace. Pro výpočet objemu kužele použijeme známý vzorec
(- poloměr základny kužele, - jeho vysoká). V našem případě dostáváme
. Konečně se dostáváme

.

Příklad 2.5. Vypočítejte oběh vektorového pole
po vrstevnici , tvořený průsečíkem ploch
A
(
). Zkontrolujte výsledek pomocí Stokesova vzorce.

Řešení. Průsečíkem těchto ploch je kružnice
,
(obr. 2.1). Směr pojezdu se obvykle volí tak, aby jím omezená oblast zůstala vlevo. Napišme parametrické rovnice obrysu :

a parametr se liší od před
. Pomocí vzorce (2.7) s přihlédnutím k (2.1) a (2.10) získáme

.

Aplikujme nyní Stokesův vzorec (2.9). Jako povrch , natažený na obrysu , můžete vzít část letadla
. Normální směr
k tomuto povrchu je konzistentní se směrem procházení obrysu . Zkroucení daného vektorového pole je vypočítáno v příkladu 2.2:
. Proto požadovaný oběh

Kde
- oblast regionu
.
- poloměr kruhu
, kde

Postup výpočtu trojného integrálu je obdobný jako odpovídající operace pro dvojný integrál. Abychom to popsali, zavedeme koncept pravidelné trojrozměrné oblasti:

Definice 9.1. Trojrozměrná oblast V ohraničená uzavřenou plochou S se nazývá regulární, pokud:

1. jakákoli přímka rovnoběžně s osou Oz a tažený vnitřním bodem oblasti protíná S ve dvou bodech;
2. celá oblast V je promítnuta do roviny Oxy do pravidelné dvourozměrné oblasti D;
3. libovolná část oblasti V, odříznutá od ní rovinou rovnoběžnou s některou ze souřadnicových rovin, má vlastnosti 1) a 2).

Uvažujme pravidelnou oblast V, ohraničenou pod a nad plochami z=χ(x,y) a z=ψ(x,y) a promítnutou na rovinu Oxy do pravidelné oblasti D, uvnitř které se x mění od a až b, omezené křivkami y=φ1(x) a y=φ2(x) (obr. 1). Definujme spojitou funkci f(x, y, z) v oboru V.

Definice 9.2. Nazvěme trojný integrál funkce f(x, y, z) nad oblastí V vyjádřením tvaru:

Trojný integrál má stejné vlastnosti jako dvojný integrál. Uvádíme je bez důkazu, protože se dokazují podobně jako v případě dvojného integrálu.

Výpočet trojného integrálu.

Věta 9.1. Trojný integrál funkce f(x,y,z) na regulární oblasti V se rovná trojnému integrálu na stejné oblasti:

. (9.3)

Důkaz.

Rozdělme oblast V rovinami rovnoběžnými s rovinami souřadnic na n pravidelných oblastí. Pak z vlastnosti 1 vyplývá, že

kde je trojný integrál funkce f(x,y,z) přes oblast.

Pomocí vzorce (9.2) lze předchozí rovnost přepsat jako:

Z podmínky spojitosti funkce f(x,y,z) vyplývá, že limita integrálního součtu na pravé straně této rovnosti existuje a je rovna trojnému integrálu. Poté překročením limitu v , získáme:

Q.E.D.

Komentář.

Podobně jako v případě dvojného integrálu lze prokázat, že změna řádu integrace nezmění hodnotu trojného integrálu.

Příklad. Vypočítejme integrál, kde V je trojúhelníkový jehlan s vrcholy v bodech (0, 0, 0), (1, 0, 0), (0, 1, 0) a (0, 0, 1). Jeho průmět do roviny Oxy je trojúhelník s vrcholy (0, 0), (1, 0) a (0, 1). Oblast je omezena zdola rovinou z = 0 a shora rovinou x + y + z = 1. Přejděme k trojnásobnému integrálu:

Ze znaménka odpovídajícího integrálu lze odečíst faktory, které na integrační proměnné nezávisí:

Křivočaré souřadnicové systémy v trojrozměrném prostoru.

1. Válcový souřadnicový systém.

Válcové souřadnice bodu P(ρ,φ,z) jsou polární souřadnice ρ, φ průmětu tohoto bodu do roviny Oxy a aplikace tohoto bodu z (obr. 2).

Vzorce pro přechod z cylindrických souřadnic na kartézské lze zadat následovně:

x = ρ cosφ, y = ρ sinφ, z = z. (9.4)

1. Sférický souřadnicový systém.

Ve sférických souřadnicích je poloha bodu v prostoru určena lineární souřadnicí ρ - vzdálenost od bodu k počátku kartézského souřadnicového systému (nebo pólu sférického systému), φ - polární úhel mezi kladným poloosa Ox a průmět bodu do roviny Oxy a θ - úhel mezi kladnou poloosou osy Oz a segmentem OP (obr. 3). V čem

Nastavíme vzorce pro přechod z kulových do kartézských souřadnic:

x = ρ sinθ cosφ, y = ρ sinθ sinφ, z = ρ cosθ. (9,5)

Jakobián a jeho geometrický význam.

Uvažujme obecný případ změny proměnných v dvojitém integrálu. Nechť je dána oblast D v rovině Oxy, ohraničená přímkou ​​L. Předpokládejme, že x a y jsou jednohodnotové a spojitě derivovatelné funkce nových proměnných u a v:

x = φ(u, v), y = ψ(u, v). (9.6)

Uvažujme pravoúhlý souřadnicový systém Ouv, jehož bod P΄(u, v) odpovídá bodu P(x, y) z oblasti D. Všechny takové body tvoří oblast D΄ v rovině Ouv, ohraničenou čára L΄. Můžeme říci, že vzorce (9.6) stanoví vzájemnou shodu mezi body oblastí D a D΄. V tomto případě přímky u = konst a

v = const v rovině Ouv bude odpovídat některým přímkám v rovině Oxy.

Uvažujme pravoúhlou plochu ΔS΄ v rovině Ouv, ohraničenou přímkami u = konst, u+Δu = konst, v = konst a v+Δv = konst. Bude odpovídat zakřivené oblasti ΔS v rovině Oxy (obr. 4). Oblasti posuzovaných oblastí budou rovněž označeny ΔS΄ a ΔS. V tomto případě ΔS΄ = Δu Δv. Najdeme oblast ΔS. Označme vrcholy tohoto křivočarého čtyřúhelníku P1, P2, P3, P4, kde

P1(x1, y1), x1 = φ(u, v), y1 = ψ(u, v);

P2(x2, y2), x2 = φ(u+Δu, v), y2 = ψ(u+Δu, v);

P3(x3, y3), x3 = φ(u+Δu, v+Δv), y3 = ψ(u+Δu, v+Δv);

P4(x4, y4), x4 = φ(u, v+Δv), y4 = ψ(u, v+Δv).

Nahraďte malé přírůstky Δu a Δv odpovídajícími diferenciály. Pak

V tomto případě lze čtyřúhelník P1 P2 P3 P4 považovat za rovnoběžník a jeho plochu lze určit pomocí vzorce z analytické geometrie:

(9.7)

Definice 9.3. Determinant se nazývá funkční determinant nebo jakobián funkcí φ(x, y) a ψ(x, y).

Přejdeme-li k limitě v rovnosti (9.7), získáme geometrický význam jakobiánu:

to znamená, že modul jakobiánu je limitem poměru ploch nekonečně malých oblastí ΔS a ΔS΄.

Komentář. Podobným způsobem můžeme definovat pojem jakobiánu a jeho geometrický význam pro n-rozměrný prostor: pokud x1 = φ1(u1, u2,…,un), x2 = φ2(u1, u2,…,un) ,…, xn = φ(u1 , u2,…, un), pak

(9.8)

V tomto případě modul jakobiánu udává limitu poměru „objemů“ malých oblastí prostorů x1, x2,..., xn a u1, u2,..., un.

Změna proměnných ve více integrálech.

Prostudujme obecný případ změny proměnných na příkladu dvojného integrálu.

Nechť je v oboru D dána spojitá funkce z = f(x,y), jejíž každá hodnota odpovídá stejné hodnotě funkce z = F(u, v) v oboru D΄, kde

F(u, v) = f(φ(u, v), ψ(u, v)). (9.9)

Zvažte integrální součet

kde integrální součet vpravo přebírá definiční obor D΄. Přejdeme-li k limitě v , získáme vzorec pro transformaci souřadnic v dvojném integrálu.

Stáhnout z Depositfiles

Trojný integrál.

Kontrolní otázky.

Trojný integrál, jeho vlastnosti.

Změna proměnných v trojném integrálu. Výpočet trojného integrálu ve válcových souřadnicích.

Výpočet trojného integrálu ve sférických souřadnicích.

Nechte funkci u= F(x, y,z) definované v omezené uzavřené oblasti PROTI prostor R 3. Rozdělme oblast PROTI náhodně na n základní uzavřené oblasti PROTI 1 , … ,PROTI n, mající objemy  PROTI 1 , …,  PROTI n respektive. Označme d– největší z průměrů oblastí PROTI 1 , … ,PROTI n. V každé oblasti PROTI k vyberte libovolný bod P k (X k , y k ,z k) a make-up integrální součet funkcí F(X, y,z)

S =

Definice.Trojný integrál z funkce F(X, y,z) podle regionu PROTI se nazývá limita integrálního součtu
, pokud existuje.

Tím pádem,

(1)

Komentář. Kumulativní součet S záleží na tom, jak je oblast rozdělena PROTI a výběr bodů P k (k=1, …, n). Pokud však existuje limit, pak nezáleží na způsobu rozdělení regionu PROTI a výběr bodů P k. Pokud porovnáte definice dvojných a trojných integrálů, snadno v nich uvidíte úplnou analogii.

Postačující podmínka pro existenci trojného integrálu. Trojný integrál (13) existuje, pokud funkce F(X, y,z) omezený v PROTI a je nepřetržitý v PROTI, s výjimkou konečného počtu po částech hladkých ploch umístěných v PROTI.

Některé vlastnosti trojného integrálu.

1) Pokud S je tedy číselná konstanta

3) Plošná aditivita. Pokud oblast PROTI rozdělena do oblastí PROTI 1 A PROTI 2, tedy

4) Objem těla PROTI rovná se

(2 )

Výpočet trojného integrálu v kartézských souřadnicích.

Nechat D projekce těla PROTI do letadla xOy, povrchy z=φ 1 (X,y),z=φ 2 (X, y) omezit tělo PROTI níže a výše. Znamená to, že

PROTI = {(X, y, z): (X, y)D , φ 1 (X,y)≤ z ≤ φ 2 (X,y)}.

Nazvěme takové tělo z- válcový. Trojný integrál (1) nad z- válcové tělo PROTI se vypočítá přechodem na iterovaný integrál sestávající z dvojitého a určitého integrálu:

(3 )

V tomto iterovaném integrálu se nejprve vyhodnotí vnitřní určitý integrál nad proměnnou z, kde X, y jsou považovány za trvalé. Potom se vypočítá dvojitý integrál výsledné funkce přes plochu D.

Li PROTI X- válcové popř y- válcové tělo, pak jsou správné následující vzorce:

V prvním vzorci D  projekce těla PROTI do souřadnicové roviny yOz, a ve druhém - do letadla xOz

Příklady. 1) Vypočítejte objem tělesa PROTI, omezený povrchy z = 0, X 2 + y 2 = 4, z = X 2 + y 2 .

Řešení. Vypočítejme objem pomocí trojného integrálu podle vzorce (2)

Přejděme k opakovanému integrálu pomocí vzorce (3).

Nechat D- kruh X 2 + y 2 ≤ 4, φ 1 (X , y ) = 0, φ 2 (X , y )= X 2 + y 2. Potom pomocí vzorce (3) získáme

Pro výpočet tohoto integrálu přejdeme k polárním souřadnicím. Zároveň kruh D promění v soubor

D r = { (r , φ ) : 0 ≤ φ < 2 π , 0 ≤ r ≤ 2} .

2) Tělo PROTI omezeno na povrchy z=y , z= –y , x= 0 , x= 2, y= 1. Vypočítejte

Letadla z = y , z = –y omezují tělo zespodu a nad rovinou x= 0 , x= 2 omezují tělo zezadu a zepředu a z roviny y= 1 omezuje doprava. V –z- válcové těleso, jeho projekce D do letadla xOy je obdélník OABC. Položme φ 1 (X , y ) = –y

Trojný integrál se zapisuje takto:

Vypočítejte trojný integrál - znamená nalezení čísla rovného objemu tělesa PROTI nebo, co je totéž - oblasti PROTI .

Téměř každý může pochopit význam výpočtu trojného integrálu „těžkou cestou“. Přesněji - „pod kůží“, a ještě přesněji - v jejích dýchacích orgánech - plicích. Bez ohledu na to, zda to víte nebo ne, v lidských plicích je přes 700 milionů alveolů – vezikulárních útvarů propletených sítí kapilár. Výměna plynů probíhá přes stěny alveol. Můžeme tedy uvažovat takto: objem plynu v plicích lze znázornit jako nějakou kompaktní oblast. A tento objem se skládá z malých objemů soustředěných v alveolech. Klíčovou roli v tomto srovnání hraje obrovské množství plicních sklípků: jak uvidíme v dalším odstavci, přes takové „obrovské množství maličkostí“ je matematicky formulován koncept trojného integrálu.

Proč se k zjištění objemu tělesa používá trojný integrál? PROTI? Nechte oblast PROTI rozdělen na n libovolné oblasti Δ protii, a toto označení znamená nejen každou malou plochu, ale i její objem. V každé takto malé oblasti je vybrán libovolný bod Mi, A F(Mi)- funkční hodnota F(M) v tomto bodě. Nyní maximalizujeme počet takových malých oblastí a největší průměr Δ protii- naopak snížit. Můžeme sestavit celočíselný součet formuláře

Pokud je funkce F(M) = F(X, y, z) je kontinuální, bude existovat integrální součet limit výše uvedený typ. Tato hranice se nazývá trojný integrál .

V tomto případě funkce F(M) = F(X, y, z) nazývá se integrovatelná doména PROTI ; PROTI- oblast integrace; X, y, z- integrační proměnné, dv(nebo dx dy dz ) - prvek objemu.

Výpočet trojného integrálu redukcí násobnosti

Stejně jako v případě dvojných integrálů se výpočet trojných integrálů redukuje na výpočet integrálů s nižší násobností.

Zvažte trojrozměrnou oblast PROTI. Pod a nad (tedy na výšku) je tato oblast omezena plochami z = z1 (X, y) A z = z2 (X, y) . Na bocích (tedy na šířku) je plocha omezena plochami y = y1 (X) A y = y2 (X) . A nakonec do hloubky (pokud se díváte na oblast ve směru osy Vůl) - povrchy X = A A X = b

Pro aplikaci přechodu na integrály s nižší násobností je nutné, aby trojrozměrná doména PROTI bylo správné. Je správné, když je přímka rovnoběžná s osou Oz, překračuje hranici kraje PROTI ne více než ve dvou bodech. Pravidelné trojrozměrné oblasti jsou například kvádr, elipsoid a čtyřstěn. Níže uvedený obrázek ukazuje pravoúhlý rovnoběžnostěn, se kterým se setkáme v prvním příkladu řešení problému.

Pro vizualizaci rozdílu mezi správností a nesprávností dodáváme, že povrchy oblasti podél výšky správné oblasti by neměly být konkávní dovnitř. Obrázek níže je příkladem nesprávné oblasti PROTI- jednolistý hyperboloid, jehož povrch je rovný, rovnoběžný s osou Oz(červená), protíná se ve více než dvou bodech.

Budeme zvažovat pouze správné oblasti.

Takže oblast PROTI- správně. Pak pro jakoukoli funkci F(X, y, z) , nepřetržitý v kraji PROTI, vzorec je platný

Tento vzorec umožňuje zredukovat výpočet trojného integrálu na sekvenční výpočet vnitřního určitého integrálu nad proměnnou z(konstantně X A y) a vnější dvojný integrál v dvourozměrné oblasti D .

Přejdeme-li od dvojného integrálu k opakovanému, získáme následující vzorec pro výpočet trojného integrálu:

Chcete-li tedy vypočítat trojný integrál, musíte postupně vyhodnotit tři určité integrály.

Tyto integrály se počítají od nejvnitřnějšího (přes proměnnou z) na nejvzdálenější (podle proměnné X). Pro snazší pochopení posloupnosti výpočtů lze tři „vnořené“ integrály zapsat následovně:

.

Již z tohoto příspěvku je zřejmé, že:

• nejprve musíte integrovat funkci F(X, y, z) podle proměnné z a vzít rovnice jako integrační limity z = z1 (X, y) A z = z2 (X, y) plochy vymezující plochu PROTI dole a nahoře;
• y y = y1 (X) A y = y2 (X) plochy vymezující plochu PROTI ze stran;
• integrujte výsledek získaný v předchozím kroku přes proměnnou X a vzít rovnice jako integrační limity X = A A X = b plochy vymezující plochu PROTI do hloubky.

Příklad 1. Pojďme od trojného integrálu k iterovanému integrálu

-

posloupnosti tří určitých integrálů. Vyhodnoťte tento iterovaný integrál.

Řešení. Výpočet iterovaného integrálu vždy začíná od posledního integrálu:

.

Spočítejme druhý integrál – nad proměnnou y:

.

X:

.

Odpověď: Tento opakovaný integrál a jeho odpovídající trojný integrál se rovnají 10.

Příklad 2 Vypočítejte trojný integrál

,

Kde PROTI- rovnoběžnostěn ohraničený rovinami X = − 1 , X = + 1 , y = 0 , y = 1 , z = 0 , z = 2 .

Řešení. Limity integrace pro všechny tři určité integrály jsou jednoznačně specifikovány rovnicemi ploch ohraničujících rovnoběžnostěn. Proto tento trojný integrál okamžitě zredukujeme na posloupnost tří určitých integrálů:

.

z

.

Počítáme integrál „uprostřed“ - nad proměnnou y. Dostaneme;

.

Nyní vypočítáme nejvzdálenější integrál - nad proměnnou X:

Odpověď: Tento trojný integrál je -2.

Příklad 3 Vypočítejte trojný integrál

,

Kde PROTIX + y + z = 1 a souřadnicové roviny X = 0 , y = 0 , z= 0. Kraj PROTI promítnutý do roviny xOy do trojúhelníku D, jak je znázorněno na obrázku níže.

Řešení. Nejprve si stanovíme hranice integrace. Pro integrál nad proměnnou z spodní hranice integrace je jednoznačně specifikována: z= 0. Abychom získali horní hranici, vyjadřujeme z z X + y + z = 1 . Dostáváme 1 - X − y. Pro integrál nad proměnnou y spodní hranice integrace je jednoznačně specifikována: y= 0. Pro získání horní hranice vyjádříme y z X + y + z = 1 , při zvažování toho z= 0 (protože čára je umístěna v rovině xOy). Dostáváme: 1 - X .

Tento trojný integrál zredukujeme na posloupnost tří určitých integrálů:

.

Počítáme nejvnitřnější integrál - nad proměnnou z s ohledem na konstanty x a y. Dostaneme:

.

y. Dostaneme:

X:

Odpověď: Tento trojný integrál je roven 1/8.

Spočítejte si trojný integrál a pak se podívejte na řešení

Příklad 4. Vypočítejte trojný integrál

,

Kde PROTI- pyramida ohraničená rovinou X + y + z = 1 a souřadnicové roviny X = 0 , y = 0 , z = 0 .

Uspořádání integračních limit při přechodu na posloupnost tří integrálů

Stává se, že studenti, kteří nemají žádné zvláštní potíže s přímým počítáním integrálů, si při přechodu z trojného integrálu na posloupnost tří určitých integrálů nemohou zvyknout na stanovení mezí integrace. Tato záležitost vyžaduje určité školení. V prvním příkladu doména integrace PROTI byl rovnoběžnostěn, u kterého je vše jasné: je ze všech stran ohraničen rovinami, což znamená, že hranice integrace jsou jednoznačně definovány rovnicemi rovin. V druhém příkladu - pyramida: zde již bylo nutné trochu více přemýšlet a vyjádřit jednu z limit z rovnice. A pokud oblast PROTI jsou omezeny nerovnými povrchy? Prostor je samozřejmě nutné určitým způsobem kontrolovat PROTI .

Začněme "hroznějším" příkladem, abychom pocítili "situaci blízko boje."

Příklad 5. Uspořádat meze integrace při přechodu z trojného integrálu, ve kterém je kraj PROTI- elipsoid

.

Řešení. Nechť střed elipsoidu je počátkem, jak je znázorněno na obrázku výše. Podívejme se na elipsoid zespodu. Zespodu je omezena plochou, což je ta část plochy elipsoidu, která se nachází pod rovinou xOy z a výsledný výraz se znaménkem mínus bude spodní hranicí integrace nad proměnnou z:

.

Nyní se podíváme na elipsoid shora. Zde je omezena plochou, což je ta část povrchu elipsoidu, která se nachází nad osou xOy. Proto potřebujeme vyjádřit z elipsoidní rovnice z a výsledný výraz bude horní mez integrace přes proměnnou z:

.

Promítání elipsoidu na rovinu xOy je elipsoid. Jeho rovnice:

Získání spodní hranice integrace přes proměnnou y, nutno vyjádřit y z elipsoidní rovnice a vezměte výsledný výraz se znaménkem mínus:

.

Pro horní hranici integrace přes proměnnou y stejný výraz se znaménkem plus:

Ohledně integrace přes proměnnou X, pak oblast PROTI do hloubky omezený rovinami. Proto jsou limity integrace přes proměnnou X mohou být reprezentovány jako souřadnice zadní a přední hranice oblasti. V případě elipsoidu to budou hodnoty délek poloos se záporným a kladným znaménkem A: X1 = − A A X2 = A .

Posloupnost integrálů pro výpočet objemu elipsoidu je tedy následující:

,

kde „yrek first“, „yrek second“, „zet first“ a „zet second“ jsou výrazy získané výše. Pokud máte chuť a odvahu spočítat tento integrál a tím i objem elipsoidu, tak zde je odpověď: 4 πabc/3 .

Následující příklady nejsou tak děsivé jako ten, o kterém jsme právě hovořili. Navíc zahrnují nejen stanovení mezí integrace, ale také výpočet samotného trojného integrálu. Otestujte si, co jste se naučili, podle řešení děsivého příkladu. Při nastavování limitů musíte stále myslet.

Příklad 6. Vypočítejte trojný integrál

pokud je integrační doména omezena rovinami X + y = 1 , X + 2y = 4 , y = 0 , y = 1 , z = 1 , z = 5 .

Řešení. Příklad „resortu“ je porovnán s příkladem 5, protože limity integrace přes „Y“ a „Z“ jsou jednoznačně definovány. Budeme se ale muset vypořádat s limity integrace přes „X“. Projekce oboru integrace do roviny xOy je lichoběžník abeceda.

V tomto příkladu je výhodnější promítnout lichoběžník na osu Oj, jinak pro výpočet trojného integrálu budete muset rozdělit číslo na tři části. V příkladu 4 jsme začali zkoumat integrační oblast zespodu a toto je obvyklý postup. Ale v tomto příkladu začneme kontrolu ze strany, nebo, je-li to jednodušší, postavíme postavu na bok a uvážíme, že se na ni díváme zespodu. Limity integrace nad "X" můžeme najít čistě algebraicky. K tomu vyjádříme „x“ z první a druhé rovnice uvedené v příkladu podmínky. Z první rovnice získáme spodní mez 1 − y, od druhé - horní 4 − 2 y. Zredukujeme tento trojný integrál na posloupnost tří určitých integrálů:

.

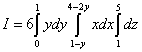Pozornost! V tomto příkladu nejvzdálenější integrál není nad proměnnou „x“, ale nad proměnnou „y“ a „průměrný“ integrál je nad proměnnou „x“! Zde jsme uplatnili změnu pořadí integrace, se kterou jsme se seznámili při studiu dvojného integrálu. Je to dáno tím, že, jak již bylo zmíněno, jsme integrační region začali zkoumat nikoli zespodu, ale ze strany, to znamená, že jsme jej nepromítali na osu Vůl, na osu Oj.

Počítáme nejvnitřnější integrál - nad proměnnou z s ohledem na konstanty x a y. Dostaneme:

Počítáme průměrný integrál - přes proměnnou X. Dostaneme:

.

Nakonec spočítáme nejvzdálenější integrál – nad proměnnou y:

Odpověď: Tento trojný integrál se rovná 43.

Příklad 7. Vypočítejte trojný integrál

,

pokud je oblast integrace omezena na povrchy X = 0 , y = 0 , z = 2 , X + y + z = 4 .

Řešení. Kraj PROTI(pyramida MNRP) je správně. Projekční plocha PROTI do letadla xOy je trojúhelník AOB.

Spodní hranice integrace pro všechny proměnné jsou uvedeny v příkladu podmínky. Pojďme najít horní hranici integrace přes "X". Za tímto účelem vyjádříme „x“ ze čtvrté rovnice, přičemž „y“ považujeme za rovné nule a „ze“ za rovné dvěma. Dostaneme X= 2. Najdeme horní hranici integrace nad „hrou“. Za tímto účelem vyjádřeme „Y“ ze stejné čtvrté rovnice, přičemž uvažujme, že „Z“ se rovná dvěma a „X“ je proměnná hodnota. Dostaneme y = 2 − X. A nakonec najdeme horní hranici integrace nad proměnnou „z“. Za tímto účelem vyjádřeme „zet“ ze stejné čtvrté rovnice, přičemž „y“ a „zet“ považujeme za proměnné veličiny. Dostaneme z = 4 − X − y .

Zredukujeme tento trojný integrál na posloupnost tří určitých integrálů:

.

Počítáme nejvnitřnější integrál - nad proměnnou z s ohledem na konstanty x a y. Dostaneme:

.

Počítáme průměrný integrál - přes proměnnou y. Dostaneme:

.

Vypočítáme nejvzdálenější integrál – přes proměnnou X a nakonec najdeme tento trojný integrál:

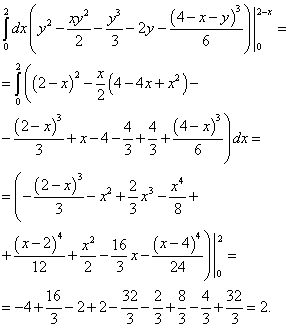
Odpověď: Tento trojný integrál je roven 2.

Změna proměnných v trojném integrálu a cylindrických souřadnicích

Je-li projekcí integrační oblasti na některou ze souřadnicových rovin kruh nebo část kruhu, pak je snazší vypočítat trojný integrál přechodem na válcové souřadnice. Válcový souřadnicový systém je zobecnění polární souřadnicový systém do vesmíru. Ve cylindrickém souřadnicovém systému bod M charakterizované třemi veličinami ( r, φ , z), kde r- vzdálenost od počátku k průmětu N body M do letadla xOy, φ - úhel mezi vektorem NA a kladný směr osy Vůl, z- aplikační bod M(obrázek níže).

Obdélníkové souřadnice X, y, z s cylindrickými souřadnicemi r, φ , z spojovat vzorce

X = r cos φ ,

y = r hřích φ ,

z = z .

Chcete-li přejít na válcové souřadnice v trojném integrálu, musíte vyjádřit integrand jako funkci proměnných r, φ , z:

To znamená, že přechod z pravoúhlých souřadnic na válcové se provádí následovně:

Trojný integrál ve válcových souřadnicích se vypočítá stejným způsobem jako v kartézských pravoúhlých souřadnicích tak, že se převede na posloupnost tří určitých integrálů:

Příklad 8. Vypočítejte trojný integrál

přechod na válcové souřadnice, kde PROTI- oblast omezená plochami a.

Řešení. Od oblasti PROTI do letadla xOy se promítá do kruhu, pak souřadnice φ se pohybuje od 0 do 2 π a souřadnice r- z r= 0 až r=1. Konstantní hodnota v prostoru odpovídá válci. Vzhledem k průsečíku tohoto válce s regionem PROTI, dostaneme změnu souřadnice z z z = r² až z= 1. Přejdeme na válcové souřadnice a dostaneme.