01.02.2022
Přímka je průsečík dvou rovin. Rovnice přímky v prostoru jsou rovnice dvou protínajících se rovin
S tímto online kalkulačka můžete najít průsečík rovin. Dáno detailní řešení s vysvětlivkami. Pro nalezení rovnice průsečíku rovin zadejte koeficienty do rovnic rovin a klikněte na tlačítko "Vyřešit". Viz teoretická část a numerické příklady níže.
×
Varování
Vymazat všechny buňky?
Zavřít Vymazat
Pokyny pro zadávání dat.Čísla se zadávají jako celá čísla (příklady: 487, 5, -7623 atd.), desetinná místa (např. 67., 102,54 atd.) nebo zlomky. Zlomek musí být zadán ve tvaru a/b, kde aab (b>0) jsou celá čísla nebo desetinná místa. Příklady 45/5, 6,6/76,4, -7/6,7 atd.
Průsečík rovin - teorie, příklady a řešení
Dvě roviny v prostoru mohou být rovnoběžné, splývat nebo se protínat. V tomto článku určíme vzájemnou polohu dvou rovin, a pokud se tyto roviny protínají, odvodíme rovnici průsečíku rovin.
Nechť je dán kartézský pravoúhlý souřadnicový systém Oxyz a nechť jsou v tomto souřadnicovém systému specifikovány roviny α 1 a α 2:
Vzhledem k tomu, vektory n 1 a n 2 jsou kolineární, pak existuje takové číslo λ ≠0, že rovnost je splněna n 1 =λ n 2, tzn. A 1 =λ A 2 , B 1 =λ B 2 , C 1 =λ C 2 .
Vynásobení rovnice (2) číslem λ , dostaneme:
Pokud rovnost D 1 =λ D 2, pak letadlo α 1 a α 2 se shodují, pokud D 1 ≠λ D 2 pak letadla α 1 a α 2 jsou rovnoběžné, to znamená, že se neprotínají.
2. Normální vektory n 1 a n 2 letadla α 1 a α 2 nejsou kolineární (obr. 2).
Pokud vektory n 1 a n 2 nejsou kolineární, pak vyřešíme soustavu lineární rovnice(1) a (2). K tomu přeneseme volné členy na pravou stranu rovnic a sestavíme odpovídající maticovou rovnici:
Kde x 0 , y 0 , z 0 , m, p, l reálná čísla a t− variabilní.
Rovnost (5) lze zapsat následující formulář:
Příklad 1. Najděte průsečík rovin α 1 a α 2:
| α 1: x+2y+z+54=0. | (7) |
Řešme soustavu lineárních rovnic (9) vzhledem k x, y, z. Abychom systém vyřešili, zkonstruujeme rozšířenou matici:
Druhá fáze. Reverzní Gaussův pohyb.
Vynechme prvky 2. sloupce matice nad prvkem A 22. Chcete-li to provést, přidejte řádek 1 k řádku 2 vynásobenému −2/5:
Dostaneme řešení:
Získali jsme rovnici průsečíku rovin α 1 a α 2 palce parametrická forma. Pojďme to napsat v kanonické podobě.
Odpověď. Rovnice průsečíku rovin α 1 a α 2 vypadá takto:
| (15) |
α 1 má normální vektor n 1 ={A 1 , B 1 , C 1) = (1, 2, 7). Rovina α 2 má normální vektor n 2 ={A 2 , B 2 , C 2 }={2, 4, 14}.
n 1 a n 2 kolineární ( n 1 lze získat násobením n 2 číslem 1/2), pak rovina α 1 a α 2 jsou paralelní nebo shodné.
α 2 vynásobeno číslem 1/2:
| (18) |
Řešení. Nejprve určíme vzájemnou polohu těchto rovin. Rovina α 1 má normální vektor n 1 ={A 1 , B 1 , C 1) = (5, -2, 3). Rovina α 2 má normální vektor n 2 ={A 2 , B 2 , C 2 }={15, −6, 9}.
Od směrových vektorů n 1 a n 2 kolineární ( n 1 lze získat násobením n 2 číslem 1/3), pak rovina α 1 a α 2 jsou paralelní nebo shodné.
Když vynásobíte rovnici nenulovým číslem, rovnice se nezmění. Převedeme rovnici roviny α 2 vynásobeno číslem 1/3:
| (19) |
Protože normální vektory rovnic (17) a (19) se shodují a volné členy jsou stejné, pak roviny α 1 a α 2 zápas.
Pokud dvě letadla protínají, pak soustava lineárních rovnic definuje rovnici přímky v prostoru.
To znamená, že přímka je definována rovnicemi dvou rovin. Typickým a běžným úkolem je přepsat rovnice přímky do kanonického tvaru:
Příklad 9
Řešení: Skládat kanonické rovnice rovně, musíte znát bodový a směrový vektor. A dali jsme rovnice dvou rovin...
1) Nejprve najděte nějaký bod patřící k dané přímce. Jak to udělat? V soustavě rovnic je potřeba vynulovat nějakou souřadnici. Nechť , pak dostaneme soustavu dvou lineárních rovnic se dvěma neznámými: . Přidáme rovnice po členech a najdeme řešení soustavy:
Bod tedy patří do této linie. Věnujte pozornost následujícímu technickému bodu: je vhodné najít bod pomocí celý souřadnice. Pokud v systému vynulujeme „X“ nebo „Z“, není pravda, že bychom získali „dobrý“ bod bez zlomkových souřadnic. Taková analýza a výběr bodu by měly být provedeny v duchu nebo na návrhu.
Zkontrolujeme: dosaďte souřadnice bodu do původní soustavy rovnic: . Jsou získány správné rovnosti, což znamená, že skutečně .
2) Jak najít směrový vektor přímky? Jeho umístění jasně ukazuje následující schematický nákres:
Směrový vektor naší přímky je ortogonální k normálovým vektorům rovin. A jestliže , pak najdeme vektor „pe“ jako vektorový produkt normální vektory: .
Z rovnic rovin odstraníme jejich normálové vektory:
A najdeme směrový vektor přímky:
Jak zkontrolovat výsledek, bylo diskutováno v článku Vektorový součin vektorů.
3) Sestavme kanonické rovnice přímky pomocí bodu a směrového vektoru:
Odpověď:
V praxi lze použít již hotový vzorec: je-li přímka dána průsečíkem dvou rovin, pak je vektor směrovým vektorem této přímky.
Příklad 10
Zapište kanonické rovnice přímky
Toto je příklad, který můžete vyřešit sami. Vaše odpověď se může lišit od mé odpovědi (v závislosti na tom, který bod zvolíte). Pokud existuje rozdíl, pak pro kontrolu vezměte bod z rovnice a dosaďte jej do mé rovnice (nebo naopak).
Úplné řešení a odpověď na konci lekce.
Ve druhé části lekce se podíváme na vzájemné polohy čar v prostoru a také analyzujeme problémy spojené s prostorovými čarami a body. Trápí mě vágní očekávání, že materiálu bude dost, takže je lepší udělat samostatnou webovou stránku.
Vítejte: Problémy s čárou v prostoru >>>
Řešení a odpovědi:
Příklad 4: Odpovědi:
Příklad 6: Řešení: Pojďme najít směrový vektor čáry:
Sestavme rovnice přímky pomocí bodu a směrového vektoru:
Odpověď
: („igrek“ – jakýkoli) :
Odpověď
:
ÚHEL MEZI ROVINAMI
Uvažujme dvě roviny α 1 a α 2 definované rovnicemi:

Pod úhel mezi dvěma rovinami budeme rozumět jednomu z dihedrálních úhlů tvořených těmito rovinami. Je zřejmé, že úhel mezi normálovými vektory a rovinami α 1 a α 2 je roven jednomu z naznačených sousedních dihedrálních úhlů popř. ![]() . Proto
. Proto  . Protože
. Protože ![]() A
A ![]() , To
, To
 .
.
Příklad. Určete úhel mezi rovinami x+2y-3z+4=0 a 2 x+3y+z+8=0.
![]()
Podmínka pro rovnoběžnost dvou rovin.
Dvě roviny α 1 a α 2 jsou rovnoběžné právě tehdy, když jsou jejich normálové vektory rovnoběžné, a proto ![]() .
.
Dvě roviny jsou tedy navzájem rovnoběžné právě tehdy, když koeficienty odpovídajících souřadnic jsou úměrné:
![]() nebo
nebo
Podmínka kolmosti rovin.
Je jasné, že dvě roviny jsou kolmé právě tehdy, když jsou jejich normálové vektory kolmé, a proto, nebo .
Tedy, .
Příklady.
ROVNĚ V PROSTORU.
VEKTOROVÁ ROVNICE PRO ČÁRU.
PARAMETRICKÉ PŘÍMÉ ROVNICE

Poloha čáry v prostoru je zcela určena určením libovolného z jejích pevných bodů M 1 a vektor rovnoběžný s touto přímkou.
Nazývá se vektor rovnoběžný s přímkou průvodci vektor této čáry.
Nechte tedy rovnou čáru l prochází bodem M 1 (x 1 , y 1 , z 1), ležící na přímce rovnoběžné s vektorem .
Zvažte libovolný bod M(x,y,z) na přímce. Z obrázku je zřejmé, že ![]() .
.
Vektory a jsou kolineární, takže existuje takové číslo t, co , kde je násobitel t může nabývat libovolné číselné hodnoty v závislosti na poloze bodu M na přímce. Faktor t nazývaný parametr. Po určení poloměrových vektorů bodů M 1 a M respektive prostřednictvím a , získáme . Tato rovnice se nazývá vektor rovnice přímky. Ukazuje, že pro každý parametr hodnotu t odpovídá vektoru poloměru nějakého bodu M, ležící na přímce.
Zapišme tuto rovnici v souřadnicovém tvaru. Všimněte si, že ![]() a odtud
a odtud
Výsledné rovnice se nazývají parametrické rovnice přímky.
Při změně parametru t změna souřadnic x, y A z a tečka M se pohybuje v přímé linii.
KANONICKÉ ROVNICE PŘÍMÉ
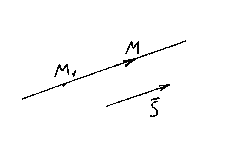
Nechat M 1 (x 1 , y 1 , z 1) – bod ležící na přímce l, A ![]() je jeho směrový vektor. Vezměme opět libovolný bod na přímce M(x,y,z) a zvažte vektor .
je jeho směrový vektor. Vezměme opět libovolný bod na přímce M(x,y,z) a zvažte vektor .
Je jasné, že vektory jsou také kolineární, takže jejich odpovídající souřadnice musí být úměrné,
![]() – kanonický rovnice přímky.
– kanonický rovnice přímky.
Poznámka 1. Všimněte si, že kanonické rovnice přímky lze získat z parametrických eliminací parametru t. Ve skutečnosti z parametrických rovnic, které získáme ![]() nebo
nebo ![]() .
.
Příklad. Zapište rovnici přímky ![]() v parametrické podobě.
v parametrické podobě.
Označme ![]() , odtud x = 2 + 3t, y = –1 + 2t, z = 1 –t.
, odtud x = 2 + 3t, y = –1 + 2t, z = 1 –t.
Poznámka 2 Nechť je přímka kolmá k jedné ze souřadnicových os, například k ose Vůl. Pak je směrový vektor přímky kolmý Vůl, tedy, m=0. V důsledku toho budou mít parametrické rovnice přímky tvar
Vyloučení parametru z rovnic t, získáme rovnice přímky ve tvaru
I v tomto případě však souhlasíme s formálním zápisem kanonických rovnic přímky do formuláře ![]() . Pokud je tedy jmenovatel jednoho ze zlomků nulový, znamená to, že přímka je kolmá k příslušné souřadnicové ose.
. Pokud je tedy jmenovatel jednoho ze zlomků nulový, znamená to, že přímka je kolmá k příslušné souřadnicové ose.
Podobně jako u kanonických rovnic ![]() odpovídá přímce kolmé k osám Vůl A Oj nebo rovnoběžně s osou Oz.
odpovídá přímce kolmé k osám Vůl A Oj nebo rovnoběžně s osou Oz.
Příklady.
OBECNÉ ROVNICE PŘÍMKY JAKO ČÁRY KŘÍŽENÍ DVOU ROVIN
Každou přímkou v prostoru prochází nespočet rovin. Jakékoli dva z nich, které se protínají, jej definují v prostoru. V důsledku toho rovnice jakýchkoli dvou takových rovin, uvažované společně, představují rovnice této přímky.
Obecně jakékoli dvě nerovnoběžné roviny dané obecnými rovnicemi

určit přímku jejich průsečíku. Tyto rovnice se nazývají obecné rovniceřídit.
Příklady.
Sestrojte přímku danou rovnicí ![]()

K sestrojení přímky stačí najít dva její body. Nejjednodušší způsob je vybrat průsečíky přímky se souřadnicovými rovinami. Například průsečík s rovinou xOy získáme z rovnic přímky za předpokladu z= 0:
Po vyřešení tohoto systému najdeme pointu M 1 (1;2;0).
Podobně za předpokladu y= 0, dostaneme průsečík přímky s rovinou xOz:
![]()

Od obecných rovnic přímky lze přejít k jejím kanonickým nebo parametrickým rovnicím. Chcete-li to provést, musíte najít nějaký bod M 1 na přímce a směrový vektor přímky.
Souřadnice bodu M 1 získáme z tohoto systému rovnic, přičemž jedné ze souřadnic přiřadíme libovolnou hodnotu. Chcete-li najít směrový vektor, poznamenejte si, že tento vektor musí být kolmý k oběma normálovým vektorům ![]() A
A ![]() . Tedy mimo směrový vektor přímky l můžete vzít vektorový součin normálních vektorů:
. Tedy mimo směrový vektor přímky l můžete vzít vektorový součin normálních vektorů:
 .
.
Příklad. Uveďte obecné rovnice přímky ![]() na kanonickou formu.
na kanonickou formu.
Najdeme bod ležící na přímce. K tomu zvolíme libovolně jednu ze souřadnic, např. y= 0 a vyřeš soustavu rovnic:
![]()
Normální vektory rovin definujících přímku mají souřadnice ![]() Proto bude směrový vektor přímý
Proto bude směrový vektor přímý
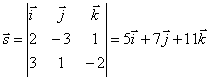 . Proto, l:
. Proto, l: ![]() .
.
ÚHEL MEZI PŘÍMKAMI
Úhel mezi přímkami v prostoru budeme nazývat libovolný ze sousedních úhlů tvořených dvěma přímkami vedenými libovolným bodem rovnoběžným s daty.
Nechť jsou v prostoru uvedeny dvě čáry:
Je zřejmé, že úhel φ mezi přímkami lze brát jako úhel mezi jejich směrovými vektory a . Od , pak pomocí vzorce pro kosinus úhlu mezi vektory dostaneme
Kanonické rovnice přímky v prostoru jsou rovnice, které definují přímku procházející daným bodem kolineárním se směrovým vektorem.
Nechť je dán bod a směrový vektor. Libovolný bod leží na přímce l pouze pokud jsou vektory a kolineární, tj. je pro ně splněna podmínka:
![]() .
.
Výše uvedené rovnice jsou kanonické rovnice přímky.
Čísla m , n A p jsou průměty směrového vektoru na souřadnicové osy. Protože vektor je nenulový, pak všechna čísla m , n A p nemůže být současně rovno nule. Ale jeden nebo dva z nich se mohou ukázat jako nula. V analytická geometrie Například je povolen následující záznam:
![]() ,
,
což znamená, že průměty vektoru na osu Oj A Oz se rovnají nule. Proto vektor i přímka definovaná kanonickými rovnicemi jsou kolmé k osám Oj A Oz, tedy letadla yOz .
Příklad 1 Napište rovnice pro přímku v prostoru kolmou k rovině ![]() a procházející průsečíkem této roviny s osou Oz
.
a procházející průsečíkem této roviny s osou Oz
.
Řešení. Najdeme průsečík této roviny s osou Oz. Od libovolného bodu ležícího na ose Oz, má souřadnice , tedy za předpokladu v dané rovnici roviny x = y = 0, dostaneme 4 z- 8 = 0 nebo z= 2. Tedy průsečík této roviny s osou Oz má souřadnice (0; 0; 2) . Protože je požadovaná přímka kolmá k rovině, je rovnoběžná se svým normálovým vektorem. Proto směrovým vektorem přímky může být normálový vektor ![]() dané letadlo.
dané letadlo.
Nyní si zapišme požadované rovnice přímky procházející bodem A= (0; 0; 2) ve směru vektoru:
![]()
Rovnice přímky procházející dvěma danými body
Přímku lze definovat dvěma body, které na ní leží ![]() A
A ![]() V tomto případě může být směrovacím vektorem přímky vektor . Poté nabývají kanonické rovnice přímky tvar
V tomto případě může být směrovacím vektorem přímky vektor . Poté nabývají kanonické rovnice přímky tvar
![]() .
.
Výše uvedené rovnice určují přímku procházející dvěma danými body.
Příklad 2 Napište rovnici pro přímku v prostoru procházející body a .
Řešení. Zapišme si požadované rovnice přímky ve tvaru uvedeném výše v teoretické literatuře:
![]()
![]() .
.
Od , pak je požadovaná přímka kolmá k ose Oj .
Přímá jako průsečík rovin
Přímku v prostoru lze definovat jako průsečík dvou nerovnoběžných rovin, tedy jako množinu bodů splňujících systém dvou lineárních rovnic.

Rovnice soustavy se také nazývají obecné rovnice přímky v prostoru.
Příklad 3 Sestavte kanonické rovnice přímky v prostoru dané obecnými rovnicemi
![]()
Řešení. Chcete-li napsat kanonické rovnice přímky nebo, což je totéž, rovnice přímky procházející dvěma danými body, musíte najít souřadnice libovolných dvou bodů na přímce. Mohou to být například průsečíky přímky s libovolnými dvěma rovinami souřadnic yOz A xOz .
Průsečík přímky a roviny yOz má úsečku x= 0. Tedy za předpokladu v této soustavě rovnic x= 0, dostaneme systém se dvěma proměnnými:
![]()
Její rozhodnutí y = 2 , z= 6 spolu s x= 0 definuje bod A(0; 2; 6) požadovaný řádek. Pak za předpokladu v dané soustavě rovnic y= 0, dostaneme systém
Její rozhodnutí x = -2 , z= 0 spolu s y= 0 definuje bod B(-2; 0; 0) průsečík přímky s rovinou xOz .
Nyní si zapišme rovnice přímky procházející body A(0; 2; 6) a B (-2; 0; 0) :
![]() ,
,
nebo po dělení jmenovatelů -2:
![]() ,
,
Podívejme se na příklad řešení.
Příklad.
Najděte souřadnice libovolného bodu na přímce definované v prostoru rovnicemi dvou protínajících se rovin  .
.
Řešení.
Přepišme soustavu rovnic do následujícího tvaru
Jako základní moll hlavní matice systému vezmeme nenulový moll druhého řádu  , to znamená, že z je volná neznámá proměnná. Přesuňme členy obsahující z na pravé strany rovnic: .
, to znamená, že z je volná neznámá proměnná. Přesuňme členy obsahující z na pravé strany rovnic: .
Připusťme , kde je libovolné reálné číslo, pak .
Vyřešme výslednou soustavu rovnic: 
Tedy obecné řešení soustavy rovnic  má tvar , kde .
má tvar , kde .
Pokud vezmeme konkrétní hodnotu parametru , pak dostaneme konkrétní řešení soustavy rovnic, které nám dá požadované souřadnice bodu ležícího na dané přímce. Tak to vezmeme  , je tedy požadovaným bodem úsečky.
, je tedy požadovaným bodem úsečky.
Nalezené souřadnice bodu můžete zkontrolovat jejich dosazením do původních rovnic dvou protínajících se rovin: 
Odpověď:
Směrový vektor přímky, podél které se protínají dvě roviny.
V pravoúhlém souřadnicovém systému je směrový vektor přímky neoddělitelný od přímky. Když je přímka a v pravoúhlém souřadnicovém systému v trojrozměrném prostoru dána rovnicemi dvou protínajících se rovin a , pak souřadnice směrového vektoru přímky nejsou vidět. Nyní si ukážeme, jak je určit.
Víme, že přímka je kolmá k rovině, když je kolmá k jakékoli přímce ležící v této rovině. Potom je normálový vektor roviny kolmý na libovolný nenulový vektor ležící v této rovině. Tyto skutečnosti využijeme k nalezení směrového vektoru přímky.
Přímka a leží jak v rovině, tak v rovině. Proto je směrový vektor přímky a kolmý na normálový vektor ![]() rovina a normální vektor
rovina a normální vektor ![]() rovina Směrový vektor přímky a je tedy
rovina Směrový vektor přímky a je tedy ![]() A
A ![]() :
:
Množina všech směrových vektorů přímky a můžeme ji definovat jako  , kde je parametr, který může nabývat jakékoli reálné hodnoty jiné než nula.
, kde je parametr, který může nabývat jakékoli reálné hodnoty jiné než nula.
Příklad.
Najděte souřadnice libovolného směrového vektoru přímky, který je v pravoúhlém souřadnicovém systému Oxyz určen v trojrozměrném prostoru rovnicemi dvou protínajících se rovin  .
.
Řešení.
Normální vektory rovin jsou vektory ![]() A
A ![]() respektive. Směrový vektor přímky, která je průsečíkem dvou daných rovin, je vektorovým součinem normálových vektorů:
respektive. Směrový vektor přímky, která je průsečíkem dvou daných rovin, je vektorovým součinem normálových vektorů: 
Odpověď:
![]()
Přechod k parametrickým a kanonickým rovnicím přímky v prostoru.
Existují případy, kdy použití rovnic dvou protínajících se rovin k popisu přímky není úplně vhodné. Některé problémy se snáze řeší, pokud známe kanonické rovnice přímky v prostoru:  nebo parametrické rovnice přímky v prostoru formuláře
nebo parametrické rovnice přímky v prostoru formuláře  , kde x 1 , y 1 , z 1 jsou souřadnice určitého bodu na přímce, a x , a y, a z jsou souřadnice směrovacího vektoru přímky a je to parametr, který nabývá libovolné reálné hodnoty. Popišme proces přechodu z lineárních rovnic tvaru
, kde x 1 , y 1 , z 1 jsou souřadnice určitého bodu na přímce, a x , a y, a z jsou souřadnice směrovacího vektoru přímky a je to parametr, který nabývá libovolné reálné hodnoty. Popišme proces přechodu z lineárních rovnic tvaru  ke kanonickým a parametrickým rovnicím přímky v prostoru.
ke kanonickým a parametrickým rovnicím přímky v prostoru.
V předchozích odstavcích jsme se naučili najít souřadnice určitého bodu na přímce a také souřadnice určitého směrového vektoru přímky, který je dán rovnicemi dvou protínajících se rovin. Tato data jsou dostatečná pro zapsání kanonických i parametrických rovnic této přímky v pravoúhlém souřadnicovém systému v prostoru.
Zvažme řešení příkladu a poté si ukážeme další způsob, jak najít kanonické a parametrické rovnice přímky v prostoru.
Příklad.

Řešení.
Vypočítejme nejprve souřadnice směrového vektoru přímky. K tomu najdeme vektorový součin normálních vektorů ![]() A
A ![]() letadla
letadla ![]() A
A ![]() :
:
To znamená, .
Nyní určíme souřadnice určitého bodu na dané přímce. K tomu najdeme jedno z řešení soustavy rovnic  .
.
Determinant  je různý od nuly, vezměme ho jako menší základ hlavní matice systému. Pak je proměnná z volná, členy s ní přeneseme na pravé strany rovnic a proměnné z dáme libovolnou hodnotu:
je různý od nuly, vezměme ho jako menší základ hlavní matice systému. Pak je proměnná z volná, členy s ní přeneseme na pravé strany rovnic a proměnné z dáme libovolnou hodnotu:
Výslednou soustavu rovnic řešíme Cramerovou metodou: 
Proto, 
Přijmeme a získáme souřadnice bodu na přímce:  .
.
Nyní můžeme zapsat požadované kanonické a parametrické rovnice původní přímky v prostoru: 
Odpověď:
![]() A
A 
Zde je druhý způsob, jak tento problém vyřešit.
Při hledání souřadnic určitého bodu na přímce řešíme soustavu rovnic  . Obecně mohou být jeho řešení zapsána ve formě
. Obecně mohou být jeho řešení zapsána ve formě  .
.
A to jsou přesně požadované parametrické rovnice přímky v prostoru. Pokud se každá z výsledných rovnic vyřeší s ohledem na parametr a pak se rovnají pravé strany rovností, získáme kanonické rovnice přímky v prostoru 
Ukažme řešení předchozího problému pomocí této metody.
Příklad.
Přímka v trojrozměrném prostoru je definována rovnicemi dvou protínajících se rovin  . Napište kanonické a parametrické rovnice pro tento řádek.
. Napište kanonické a parametrické rovnice pro tento řádek.
Řešení.
Pojďme se rozhodnout tento systém ze dvou rovnic o třech neznámých (řešení je uvedeno v předchozím příkladu, nebudeme jej opakovat). V tomto případě dostáváme  . Toto jsou požadované parametrické rovnice přímky v prostoru.
. Toto jsou požadované parametrické rovnice přímky v prostoru.
Zbývá získat kanonické rovnice přímky v prostoru: 
Výsledné rovnice přímky jsou externě odlišné od rovnic získaných v předchozím příkladu, ale jsou ekvivalentní, protože definují stejnou množinu bodů v trojrozměrném prostoru (a tedy stejnou přímku).
Odpověď:
 A
A 
Reference.
- Bugrov Ya.S., Nikolsky S.M. Algebra pro pokročilé. První díl: prvky lineární algebry a analytické geometrie.
- Ilyin V.A., Poznyak E.G. Analytická geometrie.


